Мастер-класс

Что такое числовая последовательность?

Числовая последовательность – функция вида 

y = f(x), x О N, где N– множество натуральных чисел (или функция натурального аргумента), обозначается y = f(n) или y1, y2,…, yn,…. Значения y1, y2, y3,… называют соответственно первым, вторым, третьим, … членами последовательности.

Например, для функции y = n2 можно записать:

y1 = 12 = 1;

y2 = 22 = 4;

y3 = 32 = 9;…yn = n2;…

Способы задания последовательностей

Последовательности можно задавать различными способами, среди которых особенно важны три: аналитический, описательный и рекуррентный.

1. Последовательность задана аналитически, если задана формула ее n-го члена:

yn = f(n)

Пример. yn = 2n – 1 – последовательность нечетных чисел: 1, 3, 5, 7, 9, …

2. Описательный способ задания числовой последовательности состоит в том, что объясняется, из каких элементов строится последовательность.

Пример 1. «Все члены последовательности равны 1». Это значит, речь идет о стационарной последовательности 1, 1, 1, …, 1, ….

Пример 2. «Последовательность состоит из всех простых чисел в порядке возрастания». Таким образом, задана последовательность 2, 3, 5, 7, 11, ….

3. Рекуррентный способ задания последовательности состоит в том, что указывается правило, позволяющее вычислить n-й член последовательности, если известны ее предыдущие члены. Чаще всего в таких случаях указывают формулу, позволяющую выразить n-й член последовательности через предыдущие, и задают 1–2 начальных члена последовательности.

Пример 1. y1 = 3; yn = yn–1 + 4, если n = 2, 3, 4,….

Здесь y1 = 3; y2 = 3 + 4 = 7; y3 = 7 + 4 = 11; ….

Можно видеть, что полученную в этом примере последовательность может быть задана и аналитически: yn = 4n – 1.

Пример 2. y1 = 1; y2 = 1; yn = yn–2 + yn–1 , если n = 3, 4,….

Здесь: y1 = 1; y2 = 1; y3 = 1 + 1 = 2; y4 = 1 + 2 = 3; y5 = 2 + 3 = 5; y6 = 3 + 5 = 8;

Последовательность, составленную в этом примере, специально изучают в математике, поскольку она обладает рядом интересных свойств и приложений. Ее называют последовательностью Фибоначчи – по имени итальянского математика 13 в. Задать последовательность Фибоначчи рекуррентно очень легко, а аналитически – очень трудно. n-е число Фибоначчи выражается через его порядковый номер следующей формулой .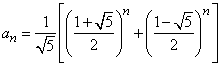

На первый взгляд, формула для n-го числа Фибоначчи кажется неправдоподобной, так как в формуле, задающей последовательность одних только натуральных чисел, содержатся квадратные корни, но можно проверить «вручную» справедливость этой формулы для нескольких первых n.

Свойства числовых последовательностей

Числовая последовательность – частный случай числовой функции, поэтому ряд свойств функций рассматриваются и для последовательностей.

Определение. Последовательность {y_n} называют возрастающей, если каждый ее член (кроме первого) больше предыдущего:

y₁ < y₂ < y₃ < … < y_n < y_n+1 < ….

Определение. Последовательность {y_n} называют убывающей, если каждый ее член (кроме первого) меньше предыдущего:

y₁ > y₂ > y₃ > … > y_n > y_n+1 > … .

Возрастающие и убывающие последовательности объединяют общим термином – монотонные последовательности.

Примеры числовой последовательности

Пример 1. y₁ = 1; y_n = n²– возрастающая последовательность.

Пример 2. y₁ = 1; 

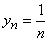 – убывающая последовательность.

Пример 3. y₁ = 1; 

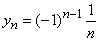 – эта последовательность не является не возрастающей не убывающей.

Определение. Последовательность называется периодической, если существует такое натуральное число T, что начиная с некоторого n, выполняется равенство y_n= y_n+T . Число T называется длиной периода.

Пример. Последовательность 

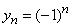 периодична с длиной периода T = 2.

Что такое арифметическая прогрессия?

Арифметическая прогрессия — это числовая последовательность вида a1,a1+d,a1+2d,...,a1+nd,...,

то есть это последовательность чисел, каждое из которых, начиная со второго, получается из предыдущего добавлением к нему постоянного числа d (разности арифметической прогрессии): an=an−1+d.

Конечный отрезок такой последовательности называется конечной арифметической прогрессией, или просто арифметической прогрессией.

Для любой пары идущих подряд членов последовательности ak и ak+1 их разность равна одному и тому же числу: ak+1−ak=d.

Например, последовательность 4,6,8,10,12 является арифметической прогрессией с разностью 2. Это возрастающая арифметическая прогрессия.

Последовательность 3,2,1,0,−1 является арифметической прогрессией с разностью −1. Это убывающая арифметическая прогрессия.

Примеры арифметической прогрессии

Пример 1. Найти сороковой член арифметической прогрессии 4;7;...

Решение:

 Согласно условию имеем

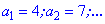Определим шаг прогрессии

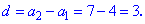По известной формуле находим сороковой член прогрессии 

: 

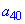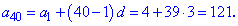
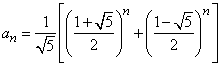
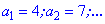
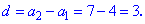
Пример 2. Арифметическая прогрессия задана третьим и седьмым ее членом  . Найти первый член прогрессии и сумму десяти.

Решение: 

Распишем заданные элементы прогрессии по формулам

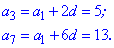
От второго уравнения вычтем первое, в результате найдем шаг прогрессии

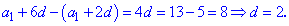
Найденное значение подставляем в любое из уравнений для отыскания первого члена арифметической прогрессии

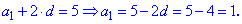
Вычисляем сумму первых десяти членов прогрессии

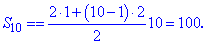
 Что такое геометрическая прогрессия?

Геометрическая прогрессия - числовая последовательность задаваемая двумя параметрами b, q (q ≠ 0) и законом , , 

Число  называют знаменателем данной геометрической прогрессии.

• Если q > 0 все члены геометрической прогрессии имеют один и тот же знак, совпадающий со знаком числа b.
• Если q < 0 знаки членов геометрической прогрессии чередуются.
• В случае -1 < q < 1 прогрессию называют бесконечно убывающей геометрической прогрессией.

Любой член геометрической прогрессии может быть вычислен по формуле:

Формула знаменателя геометрической прогрессии:

Формула суммы n-первых членов геометрической прогрессии

где, q ≠ 1

Бесконечно убывающая геометрическая прогрессия — это прогрессия, у которой |q| < 1. Для неё определяется понятие суммы членов бесконечно убывающей геометрической прогрессии как число, к которому неограниченно приближается сумма  первых членов рассматриваемой прогрессии при неограниченном возрастании числа .

Формула суммы членов бесконечно убывающей геометрической прогрессии:

где, q ≠ 1

Пример 1. Задана геометрическая прогрессия 2,6,18,... Найти десятый член прогрессии и сумму её двенадцати первых членов.